The Pohozaev identity: Semilinear elliptic problem with polygonal nonlinearity

April 11, 2010

The Pohozaev identity: Semilinear elliptic problem with polygonal nonlinearity

Filed under: PDEs — Tags: Pohozaev identities — Ngô Quốc Anh @ 12:15

Let us start with the Pohozaev identity for semilinear elliptic equation with polygonal nonlinear terms of the form

$\displaystyle -\Delta u = |u|^{p-1}u$

over an open, star-shaped domain $\Omega$ . We also assume $u$ is identical to zero on the boundary $\partial \Omega$ .

We multiply the PDE by $x \cdot \nabla u$ and integrate over $\Omega$ to find

$\displaystyle\int_\Omega {\left( { - \Delta u} \right)\left( {x \cdot \nabla u} \right)} dx = \int_\Omega {|u{|^{p - 1}}u\left( {x \cdot \nabla u} \right)} dx$ .

The term on the left is just

$\displaystyle\begin{gathered} A = - \sum\limits_{j = 1}^n {\sum\limits_{i = 1}^n {\int_\Omega {{u_{{x_i}{x_i}}}{x_j}{u_{{x_j}}}dx} } } \hfill \\ \quad= - \sum\limits_{j = 1}^n {\sum\limits_{i = 1}^n {\left[ { - \int_\Omega {{u_{{x_i}}}{{({x_j}u)}_{{x_i}}}dx} + \int_{\partial \Omega } {{u_{{x_i}}}{\nu ^i}{x_j}{u_{{x_j}}}d\sigma } } \right]} } \hfill \\ \quad= \underbrace {\sum\limits_{j = 1}^n {\sum\limits_{i = 1}^n {\int_\Omega {{u_{{x_i}}}{{({x_j}u_{x_j})}_{{x_i}}}dx} } } }_{{A_1}} - \underbrace {\sum\limits_{j = 1}^n {\sum\limits_{i = 1}^n {\int_{\partial \Omega } {{u_{{x_i}}}{\nu ^i}{x_j}{u_{{x_j}}}d\sigma } } } }_{{A_2}}. \hfill \\ \end{gathered}$

Now

$\displaystyle\begin{gathered} {A_1} = \sum\limits_{j = 1}^n {\sum\limits_{i = 1}^n {\int_\Omega {\left[ {{u_{{x_i}}}{\delta _{ij}}{u_{{x_j}}} + {u_{{x_i}}}{x_j}{u_{{x_j}{x_i}}}} \right]dx} } } \hfill \\ \quad= \int_\Omega {|\nabla u{|^2}dx} + \int_\Omega {\sum\limits_{j = 1}^n {{{\left( {\frac{{|\nabla u{|^2}}}{2}} \right)}_{{x_j}}}{x_j}} dx} \hfill \\ \quad= \int_\Omega {|\nabla u{|^2}dx} + \sum\limits_{j = 1}^n {\left[ {\int_\Omega {{{\left( {\frac{{|\nabla u{|^2}}}{2}} \right)}_{{x_j}}}{x_j}dx} } \right]} \hfill \\ \quad= \int_\Omega {|\nabla u{|^2}dx} + \sum\limits_{j = 1}^n {\left[ {\int_{\partial\Omega} {\frac{{|\nabla u{|^2}}}{2}{\nu ^i}{x_j}dx} - \int_\Omega {\frac{{|\nabla u{|^2}}}{2}dx} } \right]} \hfill \\ \quad= \int_\Omega {|\nabla u{|^2}dx} + \sum\limits_{j = 1}^n {\left[ {\int_{\partial\Omega} {\frac{{|\nabla u{|^2}}}{2}{\nu ^i}{x_j}dx} } \right]} - \sum\limits_{j = 1}^n {\left[ {\int_\Omega {\frac{{|\nabla u{|^2}}}{2}dx} } \right]} \hfill \\ \quad= \left( {1 - \frac{n}{2}} \right)\int_\Omega {|\nabla u{|^2}dx} + \int_{\partial\Omega} {\frac{{|\nabla u{|^2}}}{2}(\nu \cdot x)dx} . \hfill \\ \end{gathered}$

On the other hand, since $u=0$ on $\partial \Omega$ , $\nabla u$ is parallel to the normal at each point $x \in \partial \Omega$ . Thus

$\nabla u = \pm |\nabla u|\nu$ .

Using this equality we calculate

$\displaystyle {A_2} = \sum\limits_{j = 1}^n {\sum\limits_{i = 1}^n {\int_{\partial \Omega } {{u_{{x_i}}}{\nu ^i}{x_j}{u_{{x_j}}}d\sigma } } } = - \int_{\partial \Omega } {|\nabla u{|^2}(\nu \cdot x)d\sigma }$ .

Combining all gives

$\displaystyle A = \frac{{2 - n}}{2}\int_\Omega {|\nabla u{|^2}dx} - \frac{1}{2}\int_{\partial \Omega } {|\nabla u{|^2}(\nu \cdot x)d\sigma }$ .

We now evaluate the right hand side.

$\displaystyle\begin{gathered} B = \int_\Omega {|u{|^{p - 1}}u\left( {x \cdot \nabla u} \right)} dx \hfill \\ \quad= \sum\limits_{j = 1}^n {\int_\Omega {|u{|^{p - 1}}u{x_j}{u_{{x_j}}}} dx} \hfill \\ \quad= \sum\limits_{j = 1}^n {\int_\Omega {{{\left( {\frac{{|u{|^{p + 1}}}}{{p + 1}}} \right)}_{{x_j}}}{x_j}} dx} \hfill \\ \quad= \sum\limits_{j = 1}^n {\left[ {\int_{\partial \Omega } {\frac{{|u{|^{p + 1}}}}{{p + 1}}{\nu ^j}{x_j}} dx - \int_\Omega {\left( {\frac{{|u{|^{p + 1}}}}{{p + 1}}} \right)} dx} \right]} \hfill \\ \quad= - \sum\limits_{j = 1}^n {\left[ {\int_\Omega {\left( {\frac{{|u{|^{p + 1}}}}{{p + 1}}} \right)} dx} \right]} \hfill \\ \quad= - \frac{n}{{p + 1}}\int_\Omega {|u{|^{p + 1}}dx} . \hfill \\ \end{gathered}$

Therefore the identity becomes

$\displaystyle\frac{{n - 2}}{2}\int_\Omega {|\nabla u{|^2}dx} + \frac{1}{2}\int_{\partial \Omega } {|\nabla u{|^2}(\nu \cdot x)d\sigma } = \frac{n}{{p + 1}}\int_\Omega {|u{|^{p + 1}}dx}$ .

Definition. The following identity

$\displaystyle\frac{{n - 2}}{2}\int_\Omega {|\nabla u{|^2}dx} + \frac{1}{2}\int_{\partial \Omega } {|\nabla u{|^2}(\nu \cdot x)d\sigma } = \frac{n}{{p + 1}}\int_\Omega {|u{|^{p + 1}}dx}$

is called the Pohozaev identity for the problem $-\Delta u=|u|^{p-1}u$ .

Note that, if $\Omega$ is the star-shaped domain, we then obtain $\nu \cdot x \geqslant 0$ on $\partial \Omega$ . Consequently,

$\displaystyle\frac{{n - 2}}{2}\int_\Omega {|\nabla u{|^2}dx} \leqslant \frac{n}{{p + 1}}\int_\Omega {|u{|^{p + 1}}dx}$ .

But once we multiply the PDE by $u$ and integrate by parts, we produce the equality

$\displaystyle\int_\Omega {|\nabla u{|^2}dx} = \int_\Omega {|u{|^{p + 1}}dx}$ .

We thus conclude

$\displaystyle\left( {\frac{{n - 2}}{2} - \frac{n}{{p + 1}}} \right)\int_\Omega {|u{|^{p + 1}}dx} \leqslant 0$ .

Therefore, if $u \not \equiv 0$ , we need $p\leqslant \frac{n+2}{n-2}$ .

Comments (8)

8 Comments »

Many Thanks. This entry is nice. I have learned much.

Comment by HasPas — April 16, 2010 @ 21:49

Reply
Hi there,
First of all, thanks for these posts that help us so much. I was reading this articule and i think that in the third formula, second line (when you are using Green’s Theorem) its $u_{x_{1}}$ instead of $u$ .

Again Thanks!!

Comment by Urko — October 31, 2010 @ 7:11

Reply
- Dear Urko,
  
  Thank you for pointing out the misprint. You are right, the formula is nothing but integration by parts, that is
  
  $\displaystyle\int_\Omega {{{({u_{{x_i}}})}_{{x_i}}}({x_j}{u_{{x_j}}})dx} = - \int_\Omega {{u_{{x_i}}}{{({x_j}{u_{{x_j}}})}_{{x_i}}}dx} + \int_{\partial \Omega } {{u_{{x_i}}}{\nu ^i}{x_j}{u_{{x_j}}}d\sigma }.$
  
  Comment by Ngô Quốc Anh — October 31, 2010 @ 10:39
  
  Reply
  - In the calculation of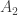 $A_2$ seems to be a mistake with the signs. Since $A=A_1-A_2$ and the sign of 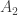$A_2$ is “-” then the formula following “Combining all gives” is wrong. Do you agree?
    
    Comment by Urko — November 1, 2010 @ 3:56
Right 😉

Comment by Urko — October 31, 2010 @ 21:28

Reply
Hi Urko,

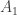Thanks again. There is no doubt in both $A$ and $A_1$ . Concerning 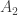$A_2$ , there is no minus sign in fact, the correct formula should be

$\displaystyle {A_2} = \sum\limits_{j = 1}^n {\sum\limits_{i = 1}^n {\int_{\partial \Omega } {{u_{{x_i}}}{\nu ^i}{x_j}{u_{{x_j}}}d\sigma } } } = \int_{\partial \Omega } {|\nabla u{|^2}(\nu \cdot x)d\sigma }$

therefore there is no mistake in the Pohozaev indentity stated in the definition.

Thanks a lot for pointing out the mistake and also for your interest in my blog.

Comment by Ngô Quốc Anh — November 1, 2010 @ 12:17

Reply
- If you have some difficulty, here is my interpretation
  
  $\displaystyle\begin{gathered} {A_2} = \sum\limits_{j = 1}^n {\sum\limits_{i = 1}^n {\int_{\partial \Omega } {{u_{{x_i}}}{\nu ^i}{x_j}{u_{{x_j}}}d\sigma } } } \hfill \\ \quad= \int_{\partial \Omega } {\sum\limits_{j = 1}^n {\sum\limits_{i = 1}^n {{u_{{x_i}}}{\nu ^i}{x_j}{u_{{x_j}}}d\sigma } } } \hfill \\ \quad= \int_{\partial \Omega } {\sum\limits_{j = 1}^n {{x_j}{u_{{x_j}}}\left( {\sum\limits_{i = 1}^n {{u_{{x_i}}}{\nu ^i}} } \right)d\sigma } } \hfill \\ \quad= \int_{\partial \Omega } {\sum\limits_{j = 1}^n {{x_j}{u_{{x_j}}}\left( { \pm |\nabla u|\nu \cdot \nu } \right)d\sigma } } \hfill \\ \quad= \int_{\partial \Omega } {\left( { \pm |\nabla u|} \right)\left( {\sum\limits_{j = 1}^n {{x_j}{u_{{x_j}}}} } \right)d\sigma } \hfill \\ \quad= \int_{\partial \Omega } {\left( { \pm |\nabla u|} \right)\left( {\nabla u \cdot x} \right)d\sigma } \hfill \\ \quad= \int_{\partial \Omega } {\left( { \pm |\nabla u|} \right)\left( { \pm |\nabla u|\nu \cdot x} \right)d\sigma } \hfill \\ \quad= \int_{\partial \Omega } {|\nabla u{|^2}(\nu \cdot x)d\sigma }. \hfill \\ \end{gathered}$
  
  Comment by Ngô Quốc Anh — November 1, 2010 @ 12:26
  
  Reply
- Thanks Ngô,
  I supposed that the mistake was in the sign of A_2 but i wasnt sure enough. Im trying to prove a Pohozaev-type identity for another equation (involving fractinal laplacians) and im using this proof as start point ;).
  
  Thanks again.
  
  Comment by Urko — November 1, 2010 @ 21:29
  
  Reply

RSS feed for comments on this post. TrackBack URI

	Earth Salt and Space… on Stereographic projection
	Ngô Quốc Anh on Extending functions between me…
	Why does Paneitz ope… on Conformal Changes of Riemannia…
	Ngô Quốc Anh on Conformal Changes of Riemannia…
	NT Tài on Conformal Changes of Riemannia…
	Calculating scalar c… on Conformal change of the Laplac…
	Poincare inequality?… on The Poincaré inequality: W^{1,…
	Implicit function th… on The implicit function theorem:…
	Heuristics for the Y… on The Yamabe problem: A Sto…
	Is there a reference… on Compact embedding of Hölder…

Ngô Quốc Anh

April 11, 2010